問題
完全に釣り合いの取れた回転円板がある。いまこの円板の中心Ｏから500mmの点Ａに小さな穴をあけたため，円板の質量が60gだけ少なくなったとする。この円板の釣り合いを回復するために，下図の点Ｂ及びＣに小さな穴をあけるとすると，Ｂ及びＣにおいてそれぞれ何gの質量を削り取らなければならないか。
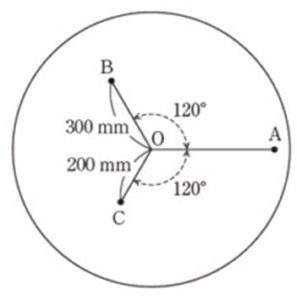
Ｂ Ｃ
⑴ 100 150
⑵ 100 80
⑶ 80 120
⑷ 120 90
⑸ 150 120
解説
釣り合いをとるためには、縦方向と横方向でそれぞれ質量×距離が等しくある必要があります。
中心Oを原点とした直交座標として、質量B、Cを求めます。
・横 3B×cos60°+2C×cos60°=5×60
・縦 3B×sin60°=2C×sin60°
3B/2+C=300
3B√3/2=2C√3/2
3B+2C=600
3B=2C
B=100
C=150
計算問題を強化したい方にオススメ
公害防止管理者 騒音・振動関係の計算問題まとめ公害防止管理者騒音・振動関係は、計算問題が多数出題されます。この記事では、「正解とヒント」など問題集を進めるため、重要な公式をまとめてい...
解答 1
次の問題だよ～♪
Ｈ30 騒音・振動特論 問18問題
ばね定数 K のばねで弾性支持されている質量M の回転機械が，ある回転数のときに鉛直方向に鋭い共振を起こす。下図に示すように，機...
前の問題だよ～♪
Ｈ30 騒音・振動特論 問16問題
JISZ8731：1999〝環境騒音の表示・測定方法〟における騒音の記述として，誤っているものはどれか。
⑴ 総合騒音とは...
ABOUT ME
この問題の解説で出てくる３Ｂ、２Cの３と２はどこから出てきましたか？
円板の中心Ｏからの距離を表しています。
点A：500mm、点B：300mm、点C：200mm
問題文のとおりに条件を考えると、以下の式になります。
・横 300B×cos60°+200C×cos60°=500×60
・縦 300B×sin60°=200C×sin60°
解説では、共通する「00」を省略しているので、上記の式とは異なっています。
わかりました。ご説明ありがとうございます。