Ｈ30　騒音・振動特論　問21

問題

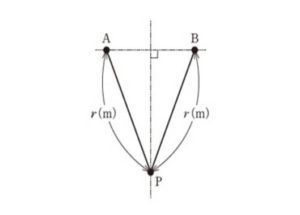
図のようにＡとＢの地表面上の点に2つの振動源がある。各振動源から距離r₀（m）離れた点での振動レベルがL₀（dB）のとき，図の同一地表面上のＰ点における振動レベルの大きさに関する記述として，正しいものはどれか。ただし，Ａ点の振動源からの振動は倍距離6dBで減衰し，Ｂ点の振動源からの振動は倍距離3dBで減衰する。また，r ＞ r₀ とする。

 

 

⑴　Ａ点からの振動の振動レベルとＢ点からの振動の振動レベルは，距離r（m）に関係なく常に同じである。

⑵　Ａ点からの振動の振動レベルが，Ｂ点からの振動の振動レベルより小さくなることはない。

⑶　Ａ点とB点からの振動の振動レベルの差は，常に3dBである。

⑷　Ｂ点からの振動の振動レベルの大きさは，L₀‐20log(r /r₀)（dB）である。

⑸　Ｂ点からの振動の振動レベルは，Ａ点からの振動の振動レベルよりも10log(r/r₀) （dB）大きい。

解説

(1)問題文で「Ａ点の振動源からの振動は倍距離6dBで減衰し，Ｂ点の振動源からの振動は倍距離3dBで減衰する。」とされているので、距離により振動レベルは変わります。

(2)問題文からA点の方が距離減衰が大きいので、離れるほどA点の方が小さくなります。

(3)(4)(5)振動の減衰は、以下の式で求められます。

L=L₀-20nlog(r/r₀)-8.7λ(r-r₀)

• L：測定点での振動加速度レベル
• L₀：基準点の振動加速度レベル
• r：発生源から測定点までの距離
• r₀：発生源から基準点までの距離
• λ：内部減衰係数
• n：幾何減衰係数

 

問題文で「Ａ点の振動源からの振動は倍距離6dBで減衰し，Ｂ点の振動源からの振動は倍距離3dBで減衰する。」とされているので、内部減衰は発生していないと考えられます。

倍距離での減衰量からA、Bでの幾何減衰係数nを求めます。

A

20nlog(2r₀/r₀)=6

20･n･0.3=6

n=1

B

20nlog(2r₀/r₀)=3

20･n･0.3=6

n=0.5

 

A、Bでの振動加速度レベルをそれぞれL_A、L_Bとして、上記の数値を代入します。

L_A=L₀-20log(r/r₀)

L_B=L₀-10log(r/r₀)

したがって、(4)はAでの加速度レベルを求める式であることが分かります。

ここから、L_AとL_Bの差は、以下のようになります。

L_B-L_A=-10log(r/r₀)+20log(r/r₀)

=-10logr+10logr₀+20logr-20logr₀

=10logr-10logr₀

=10logr/r₀

 

以上から、AとBの差は距離により変わるので、(3)は誤りであり、その差は(5)のとおり10logr/r₀となります。

 

次の問題だよ～♪

Ｈ30　騒音・振動特論　問22問題 防振ゴムに関する記述として，誤っているものはどれか。 ⑴　1個の防振ゴムで1方向だけでなく他の方向の振動絶縁にも有効である...

前の問題だよ～♪

Ｈ30　騒音・振動特論　問20問題 半無限弾性体の表面付近を伝搬する波動の振動加速度レベルに対して，距離r1（m）と r2（m）の地点のレベル差ΔL（dB）は次式で...