R5　騒音・振動特論　問4

問題

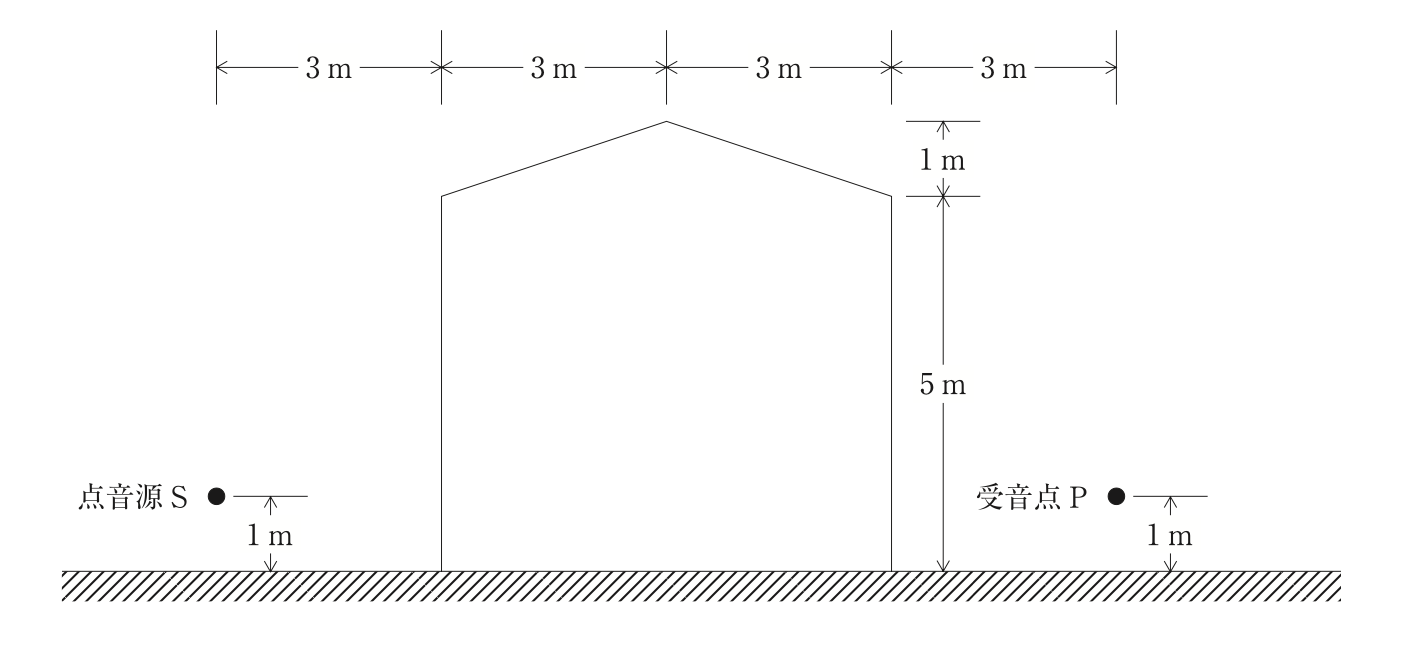
下図のように，紙面の垂直方向に長い建物と周波数 340 Hz の騒音を発する点音源 S がある。点音源 S から受音点 P に到達する騒音は，この建物の遮蔽によって約何 dB 減衰するか。なお，音速は 340 m/s とし，地表面での音の反射は無視できるものとする。

⑴ 10

⑵ 15

⑶ 20

⑷ 25

⑸ 30

難易度

△

学習の進み具合によっては知っている事項、または管理者とは別の勉強で知っている人は分かる内容であり、安定して解ければ合格率が高まる問題

解説

問3と同様、遮音壁などを迂回した場合の減衰量Rの式を使用します。

Nはフレネル数と呼ばれ、経路差を半波長で割った数値です。

音速340m/sと周波数340Hzから波長は、340/340=1.0mとなり、半波長は0.5mとなります。

ここで、経路差δを求めますが、この問題のように遮蔽物が厚い場合は、下図のように考えます。

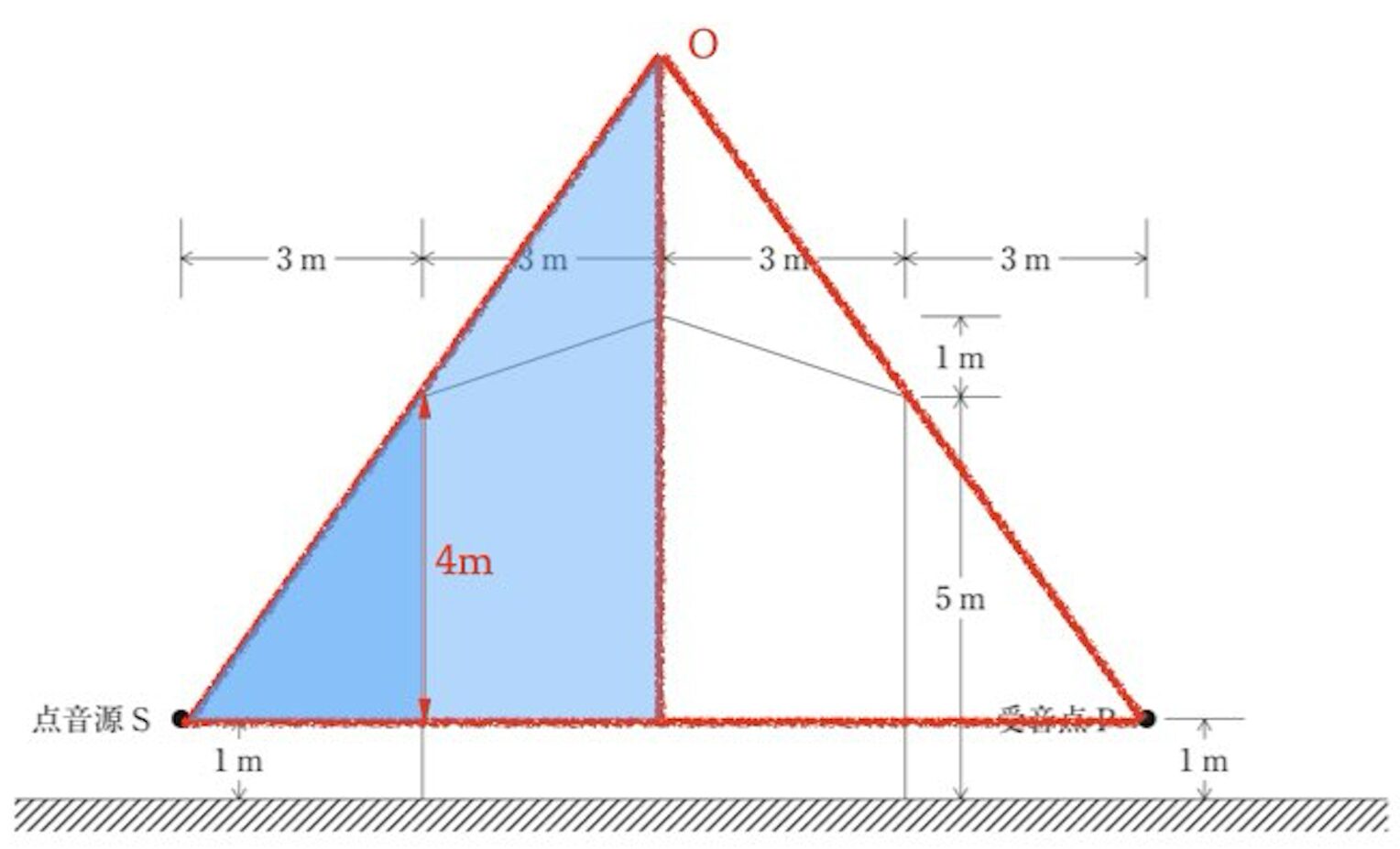
音源と受音点から建物の角に直線を伸ばし、両方の交点をOとするとき、経路差δは以下のようになります。

δ=SO+PO-SP

上の図で濃い青の三角形の辺の長さを考えます。

直角三角形で斜辺以外は3m、4mとなります。

三平方の定理から、斜辺は√(3²+4²)=5mとなります。

薄い青を含む左半分の三角形は、濃い青の三角形と相似であり、辺の長さが2倍であることから、斜辺は10mとなります。

ここから、経路差δを求めます。

δ=10+10-3×4=8

続いて、フレネル数Nを求めます。

N=8/0.5=16

以上から、減衰量Rを求めます。

R=10log16 +13=10log2⁴+13=12+13=25dB

 

---

解答．

4

---

次の問題だよ～♪

R5　騒音・振動特論　問5問題 拡散音場とみなせる部屋に音源が一つあり，その室内の平均音圧レベルが67 dB である。室内の全表面積が 410 m2，平均吸音率...

前の問題だよ～♪

R5　騒音・振動特論　問3問題 下図のように，点音源 A と受音点 B 及び C との間に，十分長い遮音塀を設置した。音速 340 m/s，周波数 680 Hz...

目次に戻るよ～♪

Ｒ5　騒音・振動特論https://pierre-usagi.com/kougai-r5-souon-shindou-tokuron-1/ https...