音響出力とは、音源が単位時間 (1秒) に放射する音響エネルギー (J)を意味します。
また、音響出力 (単位:W=J/s) をデシベル表示した量を音響パワーレベルLwと言います。
Lw(dB)=10logP/P0
- P:音響出力(W)
- P0:音響出力の基準値(=10-12W)
音響出力が分かっている音源から、一定の距離にある場所の音圧レベルは、以下の関係式で求められます。
Lp=Lw+10logQ/(4πr2)
- LW:音響パワーレベル(dB)
- r:音源からの距離(m)
- 4πr2:球の表面積
- Q:方向係数
音響パワーレベルと音圧レベルの関係は毎年問われるので、計算問題は解けるようにしましょう。
音響パワーレベルを求める問題について、以下のような質問がありました。このブログで解説している問題には無かったので、解説を作成しました。
質問
外径が各辺1mの立方体の音源が反射音を無視できる空間にある。音源の各面の中央から1m離れた点における騒音レベルはすべて70dBであった。全ての方向に一様に音波が放射と仮定したとき、この音源のA特性音響パワーレベルはおよそ何dBか?
解説
音響パワーレベルと音圧レベルの関係式は、点音源である音源と受音点までの距離についての関係を示しています。
この問題の場合、どの面からも一様に70dBが発せされていますので、実際の点音源は立方体の中心にあると考えられます。一面だけ模式図にすると、以下のようになります。
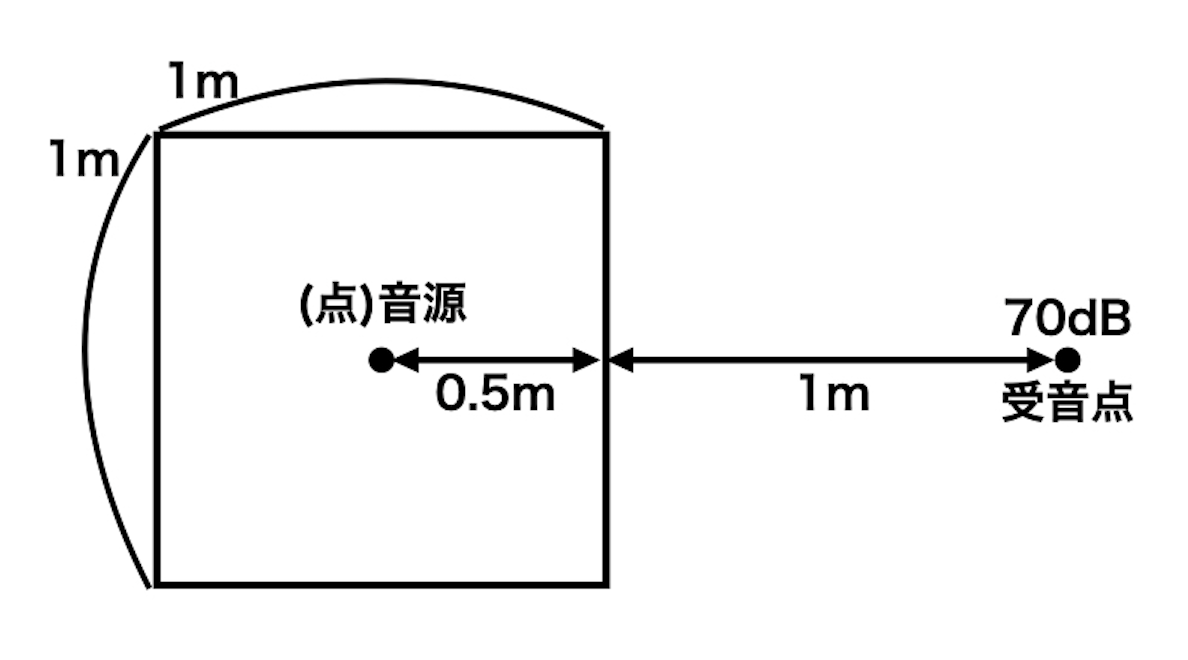
この状態を踏まえ、上記関係式に数字を代入します。
Lp=Lw+10logQ/(4πr2)
- Lp:70dB
- Q:全ての方向から音が出ているので、1
- r:0.5+1=1.5m
70=Lw+10log1/(4×3.14×1.52)
Lw=70-10log1/(4×3.14×1.52)
=70+10log(4×3.14×1.52)
=70+10log28.3
=70+14.5≒85dB
類題として、令和4年度特論7も参考になると思うので、よろしければご覧ください。






