問題
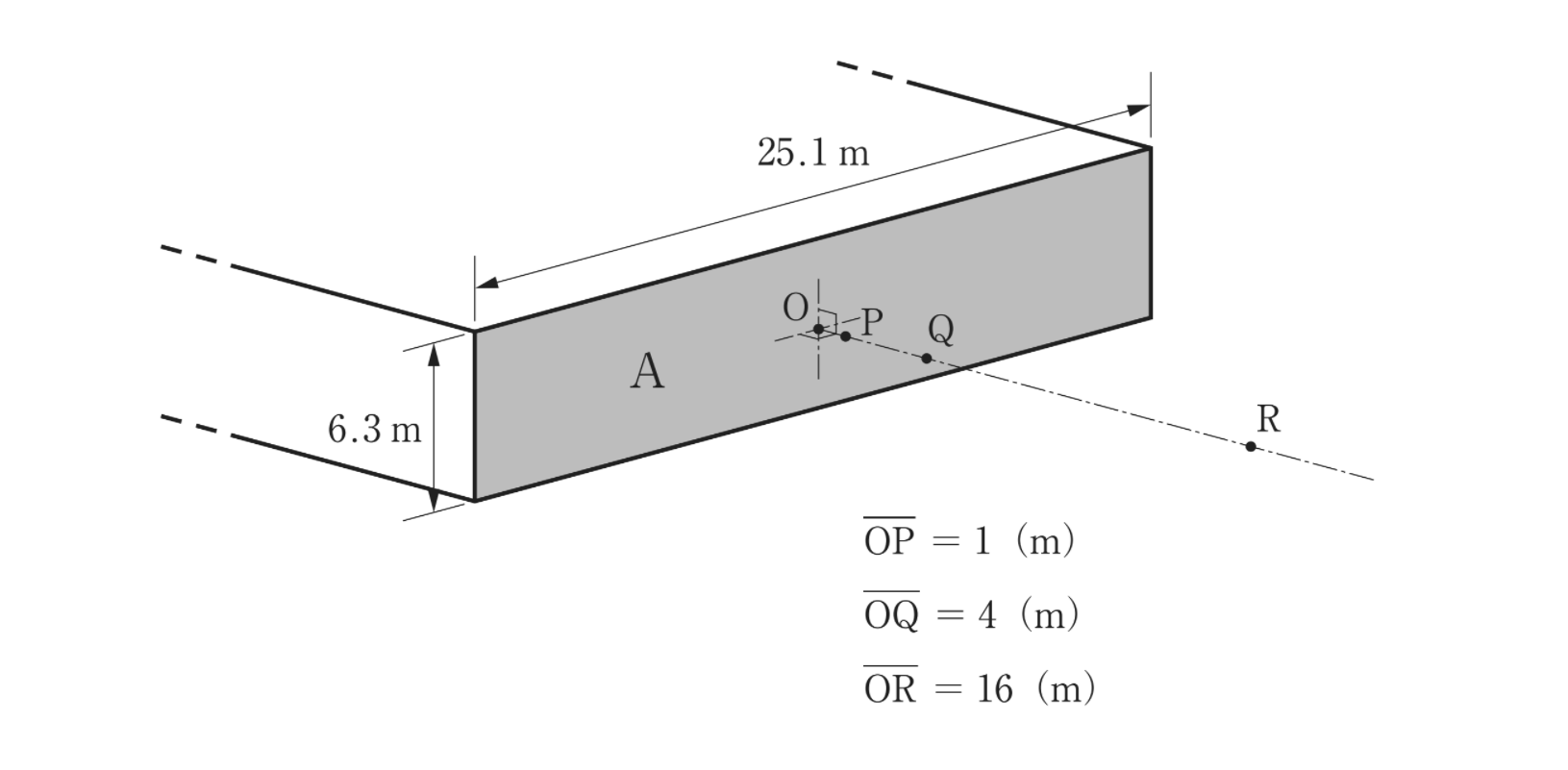
下図に示す工場建屋の壁面Ａから，外部に向かって騒音が一様に放射されてい る。この壁面の中心 O から壁面Ａに対して垂直に 1 m 離れた地点 P における騒音 レベルが 63 dB であったとき，その延長線上にある地点 Q 及び R における騒音レベルの値に最も近い組合せはどれか。ただし，壁面Ａ以外から放射される騒音，地面等における騒音の反射，及び暗騒音の影響は，いずれも無視できるものとする。
地点 Q – 地点 R
⑴ 63 – 57
⑵ 60 – 54
⑶ 60 – 51
⑷ 57 – 51
⑸ 57 – 48
解説
無限の場合、面音源は距離減衰なし、線音源は倍距離で3デシベル、点音源は倍距離で6dBの距離減衰があります。
有限で長方形の音源の場合、短辺をa、長辺をbとすると、音源からの距離により以下のように距離減衰が変化します。
～a/π•••面音源
a/π～b/π•••線音源
b/π～•••点音源
以上を踏まえて、この問題の条件を確認します。
まず、短辺6.3mから6.3/3.14≒2mで面音源から線音源に変わります。
また、長辺25.1mから25.1/3.14≒8mで線音源から点音源に変わります。
地点Pは、面音源の範囲にあるので、音源の騒音レベルは63デシベルであることがわかります。
地点Qは音源から4mなので、線音源となった地点からちょうど倍の距離になります。
線音源の距離減衰は、倍距離で3デシベルなので、63-3=60デシベルとなります。
地点Rは音源から16mなので、点音源となった地点（音源から8m）からちょうど倍の距離になります。
4mの地点Qで60デシベルだったので、音源から8mはそこからさらに倍距離で57デシベルになります。
点音源の距離減衰は、倍距離で6デシベルなので、57-6=51デシベルとなります。
解答．
3
次の問題だよ～♪
前の問題だよ～♪
目次に戻るよ～♪
