問題
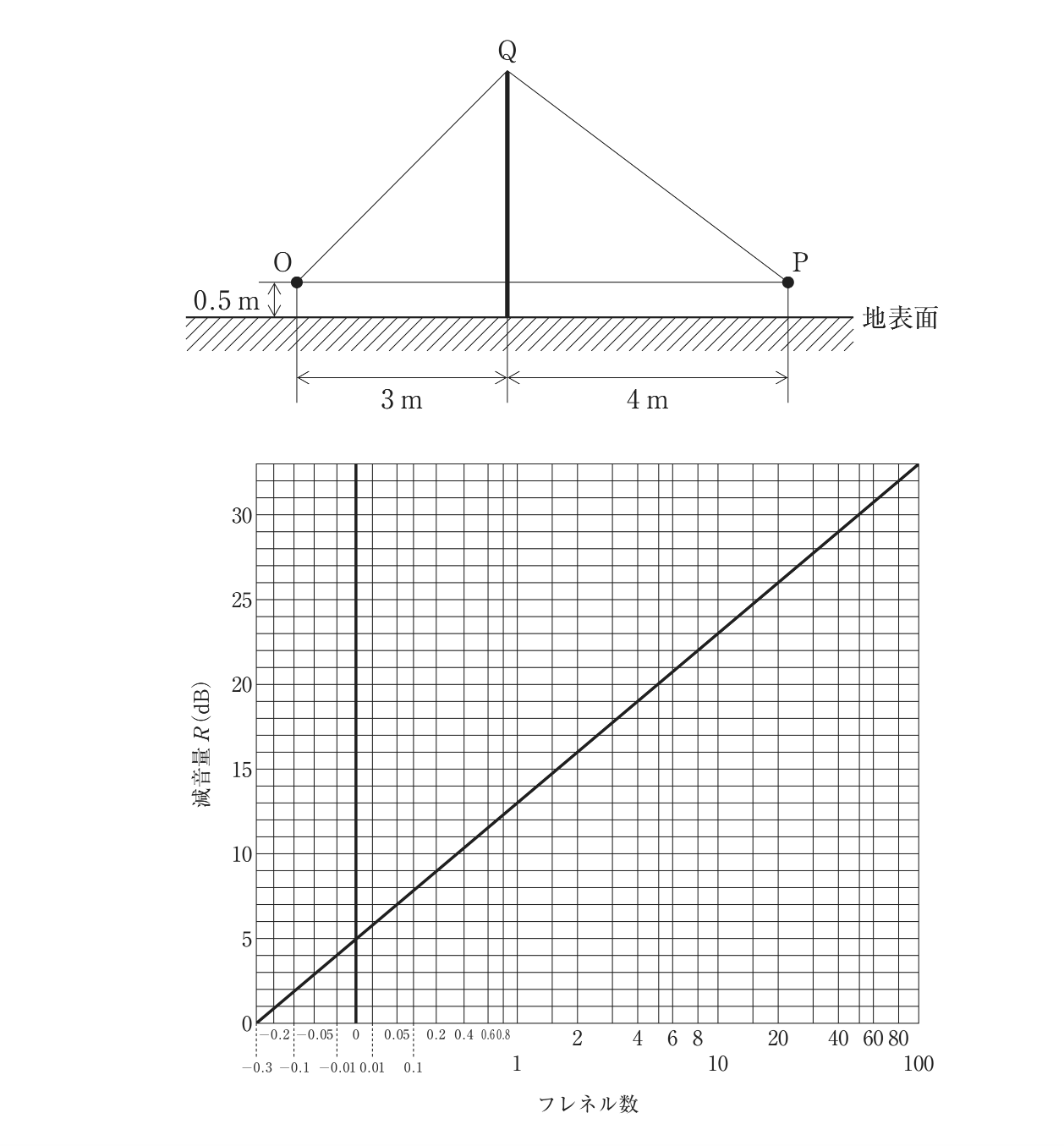
下図のように点音源 O があり，周波数 340 Hz の純音性の騒音を発している。 塀を建てることによって，その垂直断面上にある受音点 P における騒音のレベル を 16 dB 減衰させるには，塀の高さ（地表面から頂点 Q まで）を少なくとも約何 m にすればよいか。ただし，塀の長さは十分に長く，また塀からの透過音及び地表面での反射音は無視できるものとする。 √2 = 1.41， √5 = 2.24， √13 = 3.61， √17 = 4.12 として計算せよ。
⑴ 1.5
⑵ 2.5
⑶ 3.5
⑷ 4.5
⑸ 5.5
解説
表に記載されているフレネル数Nとは、音源から受音点までの直線距離と防音壁を迂回した実際の伝達距離の差を半波長で割った数字です。
まずは、音源の波長を求めます。
音速＝波長×周波数から、波長＝340/340＝1となります。
半波長＝1/2＝0.5となります。
表から、減衰量16デシベルのフレネル数Nは2であることがわかります。
各辺を以下のようにおいて、計算を進めます。
フレネル数は、経路差（a+b-3-4）を半波長で割ったものです。
2=(a+b-3-4)/0.5
a+b=8
図の三角形QOPを塀を境に直角三角形二つに分けると、三平方の定理から以下の関係が成り立ちます。
a2=32+c2⇨c2=a2-9•••①
b2=42+c2⇨c2=b2-16•••②
したがって、a2-9=b2-16となります。
a+b=8から、b=8-aを代入します。
a2-9=(8-a)2-16
a2-9=a2-16a+64-16
16a=57
a=57/16≒3.56
これを①に代入します。
c2=a2-32=3.562-32=3.67
c=1.9
元々、cは地面から0.5mの高さなので、塀は1.9+0.5=2.4mとなり、一番近い選択肢は2となります。
また、選択肢の数字をa、b、cの関係式に代入しても同じく求まります。
計算でゴリ押し感のある問題でしたが、実際の試験では計算時間が採れるかわかりません。
余った時間で計算する、選択肢を利用するなど、時間を気にしながら解く問題であると感じます。
解答．
2
次の問題だよ～♪
前の問題だよ～♪
目次に戻るよ～♪
