公害防止管理者 騒音・振動関係の計算問題まとめ

公害防止管理者騒音・振動関係は、計算問題が多数出題されます。この記事では、「正解とヒント」など問題集を進めるため、重要な公式をまとめています。

また、移動中などに覚えたい方向けに、Youtubeに動画もアップしています。
- 対数計算の基礎
- 周波数f(Hz)、周期T(s)
- 音速c(m/s)、周波数f(Hz)、波長λ(m)
- 角周波数ω(rad/s)、加速度a(m/s2)、速度v(m/s)、変位y(m)
- うなり
- 入射角と屈折角
- 平均聴力レベル
- デシベルdBの和の補正値
- デシベルの平均(等価騒音レベル、等価振動レベル)
- 時間率騒音レベル、時間率振動レベル
- 時間帯補正等価騒音レベル
- 音圧レベル・騒音レベル
- A特性の補正値
- 音圧実効値、音の強さ
- 音の強さIと音響出力P
- 音の強さIのレベル
- 音響パワーレベル
- 音圧レベルと音響パワーレベルの関係(直接音)
- 音圧レベルと音響パワーレベルの関係(反射音)
- 音の大きさ(ラウドネス)と音の大きさのレベル
- 音源からの距離ごとの面音源、線音源、点音源
- 点音源からの距離減衰
- 線音源からの距離減衰
- 吸音ダクト形消音器の伝達損失
- 膨張形消音器の伝達損失
- 干渉形消音器
- 遮音塀による減衰量
- 室内の平均音圧レベル
- セイビンの残響公式
- 吸音率と反射率
- 音響透過損失
- 総合音響透過損失
- 壁の音響透過損失
- 吸音率が最大となる空気層の厚さ
- 穴あき板による吸音機構の固有周波数
- ヘルムホルツの共鳴器の固有周波数
- オクターブバンド、1/3オクターブバンド
- 周波数分解能
- 振動加速度レベル、振動レベル
- 振動感覚補正値
- 加速度、速度、変位の関係
- 正弦振動の実効値
- 固有角振動数、ばね定数、質量の関係
- ばね定数の和
- 固有振動数、静的たわみの関係
- 減衰比
- 共振の鋭さ
- 振動伝達率
- 弾性支持をしているときの振動伝達率
- 質量付加前後の振動伝達率
- 振動の距離減衰
- 地盤の固有振動数
対数計算の基礎

周波数f(Hz)、周期T(s)
f=1/T
音速c(m/s)、周波数f(Hz)、波長λ(m)
c=f×λ
音速と温度は、以下の関係があります。
c=331.5+0.61×θ
- c:音速(m/s)
- θ:温度(℃)
過去問.




角周波数ω(rad/s)、加速度a(m/s2)、速度v(m/s)、変位y(m)
ω=2πf
a=ωv=ω2y
v=ωy=2πf・y
- 速度は変位に対して90°進んでいます。
- 加速度は変位に対して180°進んでいます(変位と逆位相)。
うなり
|f1-f2|
入射角と屈折角
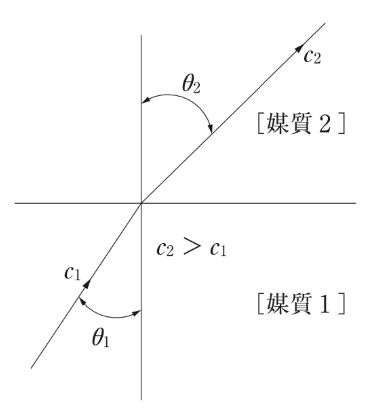
sinθ1/sinθ2=c1/c2
平均聴力レベル
・三分法平均聴力レベル (A+B+C)/3
・四分法平均聴力レベル (A+2B+C)/4
・新四分法平均聴力レベル (A+B+C+D)/4
・六分法平均聴力レベル (A+2B+2C+D)/6
- A:500 Hz の聴力レベル
- B:1000 Hz の聴力レベル
- C:2000 Hz の聴力レベル
- D:4000 Hz の聴力レベル
過去問.



デシベルdBの和の補正値
| レベル差(dB) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10~ |
| 補正値(dB) | 3 | 2 | 1 | 0 | |||||||
実際の問題では、オクターブバンドごとに音圧レベルや振動加速度レベルが与えられ、バンドごとのレベルを合計し、騒音レベルや振動レベルを求めます。
対数の足し算で精密に求めることも可能ですが、試験では、この補正値で概算が分かれば正解できます。
限られた試験時間内で、早く解くテクニックになるので、和の補正値は必ず覚えましょう。
過去問.











デシベルの平均(等価騒音レベル、等価振動レベル)
(等価騒音レベルLAeq、等価振動レベル)=(デシベルの和)-10 log n
- nは個数
等価騒音レベルLAeq=(個々の等価騒音レベル)+10 log t/T
- t:個々の平均化時間
- T:平均化時間
単発騒音暴露レベルとは、1秒あたりの騒音レベルです。
過去問.










時間率騒音レベル、時間率振動レベル
- 変動騒音:90パーセントレンジの上端(L5)
- 変動振動:80パーセントレンジの上端(L10)
90パーセントレンジとは、全測定値のうち最大レベルから上位5%、最小レベルから下位5%を除き、残った90%を意味します。
過去問.





時間帯補正等価騒音レベル
等価騒音レベルに対する補正値
- 昼間:補正なし
- 夕方:+5(dB)
- 夜間:+10(dB)
時間帯補正等価騒音レベル(Lden)とは、等価騒音レベルを昼、夕、夜間ごとに補正して評価するものです。航空機騒音の環境基準の測定で用いられます。
過去問.


音圧レベル・騒音レベル
L=20 log p/p0
- p:音圧(Pa)
- 音圧レベルの場合は、音圧実効値
- 騒音レベルの場合は、周波数重みA特性をかけた音圧実効値
- p0:基準音圧(Pa)=2×10-5Pa
実効値は、正弦波の振幅を1/√2倍した値です。
音圧実効値(Pa)から、音圧レベルや騒音レベル(dB)を求められるようにしましょう。
過去問.





A特性の補正値
| 周波数(Hz) | 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 |
| 補正値(dB) | -26 | -16 | -9 | -3 | 0 | +1 | +1 | -1 |
表の周波数は、オクターブバンド中心周波数です。
実際の問題では、この周波数ごとに音圧レベルが与えられ、A特性で補正したレベルを合計し、騒音レベルを求めます。
私の場合は、周波数の順番に合わせ、補正値も同じ順で覚えています。
26、16、9、3、ゼロ、プラス1、プラス1、マイナス1
2000ヘルツ、4000ヘルツは、プラスなので、注意してください。
過去問.









音圧実効値、音の強さ
音圧実効値p(Pa)=ρcν
音の強さI(W/m2)=p2/ρc
- ρ:空気の密度(≒1.2kg/m3)
- c:音速(≒340m/s)
- ρc:特性インピーダンス(1.2×340≒400Pa・s/mと与えられることが多い)
- ν:粒子速度(m/s音速ではなく、空気の粒子の速度)
過去問.




音の強さIと音響出力P
音の強さI(W/m2)=P/(4πr2)・Q
- P:音響出力(W)
- r:音源からの距離(m)
- 4πr2:球の表面積
- Q:方向係数
音の強さIのレベル
音の強さI(W/m2)のレベル(dB)=10logI/I0
- I0:基準の音の強さ(=10-12W/m2)
過去問.


音響パワーレベル
音響パワーレベル(dB)=10logP/P0
- P:音響出力(W)
- P0:音響出力の基準値(=10-12W)
過去問.


音圧レベルと音響パワーレベルの関係(直接音)
Lp=Lw+10logQ/(4πr2)
- Lp:音圧レベル(dB)
- Lw:音響パワーレベル(dB)
- Q:方向係数
- r:音源からの距離(m)
方向係数は、音源に対して全方位何も遮られていない場合(自由空間)を1とし、区切りに応じて数字が上がります。半自由空間の床面は、空間が半分に区切られているので2となります。
過去問.






音圧レベルと音響パワーレベルの関係(反射音)
Lp=Lw+10log4/R
- R:室定数(m2)
室定数Rとは、室の吸音性を表す数値で、以下の式で求められます。
R=A/(1-α)=αS/(1-α)
- A:等価吸音面積(S×α)(m2)
- S:室の表面積(m2)
- α:平均吸音率
過去問.



音の大きさ(ラウドネス)と音の大きさのレベル
Ls=33.2logS+40
- Ls:音の大きさレベル(phon)
- S:音の大きさ(sone)
音の大きさ(ラウドネス)は、感覚的にどれくらい大きいかの指標であり、単位はソーン(sone)です。
過去問.





音源からの距離ごとの面音源、線音源、点音源
面音源の範囲: 距離が 短辺/π以下
線音源の範囲: 距離が 短辺/πから 長辺/πの間
点音源の範囲: 距離が 長辺/π以上
面音源は、距離による音圧低下がない。
過去問.



点音源からの距離減衰
L1-L2=20logr2/r1
- L1:r1での音圧レベル(dB)
- L2:r2での音圧レベル(dB)
- r1、r2:音源からの距離
距離が倍(r2=2×r1)になったときの減衰
20log2×r1/r1=20log2=6dB
過去問.



線音源からの距離減衰
L1-L2=10logr2/r1
- L1:r1での音圧レベル(dB)
- L2:r2での音圧レベル(dB)
- r1、r2:音源からの距離
距離が倍(r2=2×r1)になったときの減衰
10log2×r1/r1=20log2=3dB
長さ l の有限長線音源の距離減衰特性は,l/π 以遠で倍距離で6dBとなります。
吸音ダクト形消音器の伝達損失
R=(α-0.1)・P・l/S
- R:伝達損失(dB)
- α:吸音率
- P:ダクトの周長(m)
- l:ダクトの長さ(m)
- S:ダクトの断面積(m2)
過去問.




膨張形消音器の伝達損失
R=10log[1+1/4・{m-(1/m)}2×sin2(kl)]
- R:伝達損失(dB)
- m:膨張比(断面積の比率)
- k:波長定数rad/m(2πf/c)
- l:空洞の長さ
Rが最大となるとなるのは、klが90度(π/2)、270度(3π/2)、450度(5π/2)…のときとなる。
特にπ/2のときの周波数fは、c/(4l)となる。
過去問.







干渉形消音器
l1 – l2 =λ/2=c/2f
- l1、l2:消音器の経路(m)(l1>l2)
- λ:波長(m)
- c:音速(m/s)
- f:周波数(Hz)
この式のように通路が半波長ずれた状態の音を重ねることが出来れば、ちょうど打ち消し合うことができます。
過去問.


遮音塀による減衰量
R=10logN +13
- R:遮音塀を迂回した音の減衰量(dB)
- N:フレネル数(経路差δを半波長λ/2で割った数値)
経路差δとは、音源と受音点の直線距離、音源と受音点の遮音壁を迂回した距離の差です。
正確には、フレネル数により以下の関係となります。
- R=10logN+13 (1≦N)
- R=5+8√(N) (0<N<1)
- R=5-8√(N) (-0.36≦N<0)
過去問.











室内の平均音圧レベル
Lp=Lw+10log4/A
- Lp:室内の平均音圧レベル(dB)
- Lw:音響パワーレベル(dB)
- A:等価吸音面積=S(表面積m2)×α(吸音率)
過去問.





セイビンの残響公式
T=0.161V/α平均S総
- T:残響時間
- V:室容積
- α平均:平均吸音率
- S総:総表面積
残響時間とは、音が停止してから室内の平均音圧レベルが60デシベル減少するまでにかかる時間です。
平均吸音率αを求める式は、以下のようになります。
α平均=ΣαS /ΣS=ΣαS/S総
過去問.




吸音率と反射率
(吸音率)=1-(反射率)
過去問.


音響透過損失
音響透過損失TL(dB)=10log1/τ
- τ:透過率
総合音響透過損失
総合音響透過損失(dB)=10log{S1+S2+S3+…}/{S1×τ1+S2×τ2+S3×τ3…}
- S:面積m2
- τ:透過率
過去問.



壁の音響透過損失
ランダム入射音響透過損失TL(dB)= 18log10(mf)- 44
垂直入射音響透過損失TL0(dB)= 20log10(mf)- 42.5
- m:遮音材料の面密度(kg/m2)
- f:入射音の周波数(Hz)
この式の内、面密度m(kg/m2)は、密度ρ(kg/m3)、壁の厚さt(m)とすると、m=ρtと表せます。
過去問.




吸音率が最大となる空気層の厚さ
d=λ/4
- d:空気層の厚さ(m)
- λ:波長(m)
過去問.


穴あき板による吸音機構の固有周波数
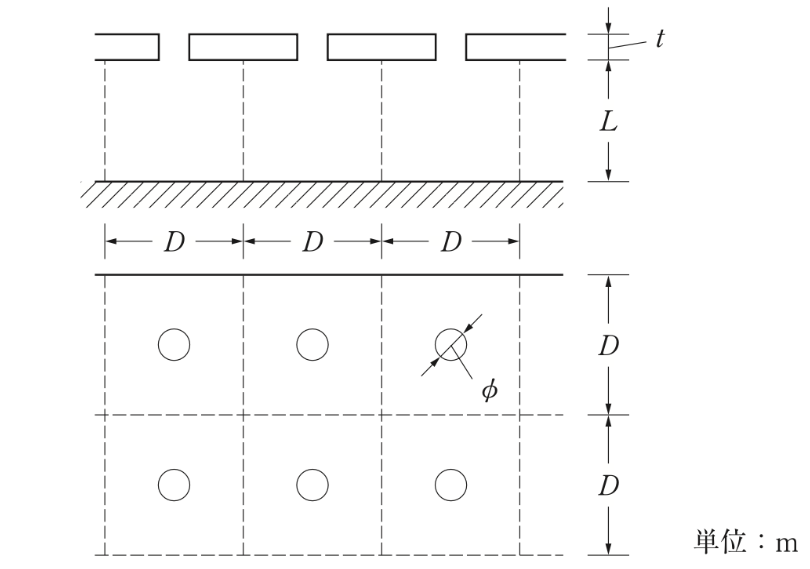
f0=c/2π・√(P/(t+0.8φ)L)
- f0:固有周波数(Hz)
- c:音速(m/s)
- P:開口率
- t:板厚
- φ:口径
- L:空気層の深さ
過去問.


ヘルムホルツの共鳴器の固有周波数
f0=c/2π√(S/Vl)
- f0:固有周波数(Hz)
- c:音速(m/s)
- V:容積(m3)
- S:内断面積(m2)
- l:管の長さ(m)
オクターブバンド、1/3オクターブバンド
オクターブバンドにおける下限周波数f1と上限周波数f2の関係
2×f1=f2
fm=√(f1・f2)=√2・f1=f2/√2
- 中心周波数fm
- オクターブバンドにおける下限周波数f1、上限周波数f2
1/3オクターブバンドにおける下限周波数f1と上限周波数f2の関係
3√2・f1=f2
fm=√(f1・f2)=6√2・f1=f2/6√2
- 3√2=1.25
- 6√2=1.12
過去問.









周波数分解能
(周波数分解能)=(サンプリング周波数)/(FFT ポイント数)
振動加速度レベル、振動レベル
振動加速度レベルLa(dB)、振動レベルLv(dB)=20loga/a0
- a:振動加速度の実効値(m/s2)
- a0:基準の振動加速度(10-5m/s2)
振動加速度レベルに水平・鉛直特性で補正したものが振動レベルになります。
過去問.


振動感覚補正値
| 周波数(Hz) | 1 | 2 | 4 | 8 | 16 | 31.5 | 63 |
| 鉛直方向の補正値(dB) | -6 | -3 | 0 | -1 | -6 | -12 | -18 |
| 水平方向の補正値(dB) | 3 | 2 | -3 | -9 | -15 | -21 | -27 |
表の周波数は、オクターブバンド中心周波数です。
実際の問題では、この周波数ごとに振動加速度が与えられ、感覚補正値で補正したレベルを合計し、振動レベルを求めます。
私の場合は、周波数の順番に合わせ、補正値も同じ順で覚えています。
- 鉛直方向について、6、3、ゼロ、1、あとは6の倍数。
- 水平方向について、3、2、3、9、あとは6ずつマイナス。
水平方向の1、2ヘルツはプラスなので、注意してください。
振動感覚補正値は、鉛直方向は規制値の測定に使用されるので、必ず覚えましょう。
また、水平方向も、鉛直方向ほどではないですが、試験で問われます。
過去問.






















加速度、速度、変位の関係
加速度a(m/s2)=2πf×速度v(m/s)=(2πf)2×変位y(m)
- f:振動数(Hz)
加速度の位相は、速度に対して π/2、変位に対して π のずれがあります。
正弦波の基本的な性質は、以下の式で表されます。
y=y0sin[2π(x/λ+f•t)+φ]
- y:変位
- y0:最大変位
- 2πf:角振動数ω
- f:周波数
- t:時間
- x:振動源からの距離
- λ:波長
- φ:位相角
過去問.






正弦振動の実効値
A /√2
- A:振幅
√(1/T ∫0T y2dt)
- y:加速度の瞬時値
- T:時刻
過去問.



固有角振動数、ばね定数、質量の関係
固有角振動数ω0(rad/s)=√(k/m)
- k:ばね定数(N/m)
- m:質量(kg)
ω=2πfから、
固有振動数f0=1/2π×ω0=1/2π・√(k/m)
質量Mの機械をばね定数Kのばねを介して据え付けたとき、ばね定数kの動吸振器により質量mを付加した場合、以下の条件で防振します。
K/M=k/m
過去問.







ばね定数の和
直列(ばね同士がつながっている状態)→逆数を合計する
- 1/k=1/k1+1/k2+・・・
並列(ばねが横に並んでつながっている状態)→そのまま合計する
- k=k1+k2+・・・
固有振動数、静的たわみの関係
固有振動数f0=1/2π×√(g/σ)
- g:重力加速度9.8m/s2
- σ:静的たわみ(m)
過去問.


減衰比
ζ=c/cc
- ζ:減衰比
- c:ダンパーの減衰係数
- cc:臨界減衰係数(一定値)=2√mk
- m:おもりの質量
- k:ばねのばね定数
減衰比が1未満のときは、減衰する振動が発生します。
一方、減衰比が1以上のときは振動が発生しません。
過去問.


共振の鋭さ
Q= 1/(2ζ)
- Q:共振の鋭さ
過去問.


振動伝達率
τ=[{1+(2ζη)2}/{(1-η2)2+(2ζη)2}]1/2
- τ:振動伝達率
- η:振動数比f/f0
- f:加振力の振動数
- f0:固有振動数
- ζ:減衰比
次の弾性支持をしているときの振動伝達率は、減衰比ζ=0であり、減衰がないばねと重りで防振している状態です。
過去問.


弾性支持をしているときの振動伝達率
振動伝達率τ=1/{(f/f0)2-1}
- τ:振動伝達率
- f:加振力の振動数
- f0:固有振動数
→上式を変形して固有振動数を求めると、以下のようになります。
f0=f/√(1/τ +1)
振動伝達率を一定の値に変化させるために必要なばね定数を求める問題がよく出題されます。この場合、f0=f/√(1/τ +1)とf0=1/2π・√(k/m)を組み合わせて考えます。
過去問.









質量付加前後の振動伝達率
m×τ/(τ+1)=m’×τ‘/(τ’+1)
- m:元の質量
- m’:付加後の質量
- τ:振動伝達率
- τ’:付加後の振動伝達率
振動の距離減衰
L=L0-20nlogr/r0-8.7λ(r – r0)
- L0:基準点での振動加速度レベル
- r0:発生源から基準点までの距離
- r:発生源から測定点までの距離
- λ:地盤の内部減衰係数
- n:幾何減衰係数(表面波:0.5、表面波と実体波が混在:0.75、実体波:1.0、表面を伝搬する実体波:2.0)
λは地盤の内部減衰係数と呼ばれ、以下の式で表されます。
λ=2πfh/V
- f:振動数
- h:土の内部減衰係数
- V:伝搬速度
過去問.













地盤の固有振動数
f=V/4H
- f:地盤の固有振動数(Hz)
- V:横波の伝搬速度(m/s)
- H:やわらかい層の厚さ(m)
かたい層の上に H m のやわらかい層(横波の伝搬速度 V m/s)が地表まで堆積しているとき、この地盤の固有振動数f Hz を求める式です。
過去問.







-640x360.jpg)
吸音ダクト形消音器の伝達損失の公式にダクト長さがないです。
ご指摘ありがとうございます。
修正しましたので、ご確認ください。
お返事遅くなりました。
修正確認しました。
私事ですが先日、騒音振動を受験してきました。
自己採点ですが無事合格見込です。
過去問の解説ありがたかったです。
ありがとうございました!
R4年騒音振動試験の解説を是非お願いします!
順次作成していますので、しばらくお待ち下さい!
とうとう明日が試験日ですが公害こむのおかげで合格できそうです。
テキストや過去問集の解説はどうも文章が無機質で、頭が理解を拒むのですが、ピエうささんの人間臭さの香る解説のおかげで脳が情報を歓迎しました。
騒音振動の学習は周りに頼れる人がいず、他の「公害防止管理者」解説サイトでも取り扱っていないので本当に助かりました。
だいぶ気が早いですがお礼申し上げます。
私見ですが今日まで騒音振動の勉強してて思ったことを徒然と書かせていただきたく。
貴ブログ運営の参考にしていただければ幸いです。
①対数の扱いに慣れているかどうかで難易度は大きく変わる
「Logの中身の指数をLogの外に出せる」
「Logの外の係数をLogの中身の指数にできる(右肩に乗せられる)」
を理解しているとかなり楽になる
公式の言わんとする本質が見えて覚えやすくなる
覚える必要のない公式も見えてくる
②常用対数の1~10を丸暗記してるとかなり楽になる
Log1 = 0
Log2 ≒ 0.3
Log3 ≒ 0.5 (もう少し精度がいるなら0.48)
Log4 ≒ 0.6
Log5 ≒ 0.7
Log6 ≒ 0.8 (もう少し精度がいるなら0.78)
Log7 ≒ 0.85
Log8 ≒ 0.9
Log9 ≒ 0.95
Log10= 1
Logπ≒ 0.5
精度はこの程度で十分
これだけ覚えてたら常用対数表に頼る必要はほとんどない
また、各種公式の理解にも繋がる
「点音源から倍距離離れる毎に-6dBってのは音のエネルギーが1/4になるから -10Log4 = -10×0.6 = -6dB ってことか」
「50dB +50dB = 53dBってのは音のエネルギーが倍になるから 10Log2 = 10×0.3 = +3dB ってことか」
「-11dBってよくでてくるけど 10Log(1/4π) のことか」
など
③振動の距離減衰の式が覚えにくい
テキストでも基本的に
L=L0-20nLog(r/r0) -8.7λ(r – r0)
の形で載ってるが、Logの係数の「-2n」を中身に移して、r/r0の分母分子も入れ替えて-1乗を外して
L=L0 +10Log(r0/r)^2n -8.7λ(r – r0)
の形にした方が覚えやすく、式の主張も見えやすいと思う
Logの中身は「距離の2n乗に比例して減衰する」を意味し、音の拡散の「Q/4πr^2(距離の2乗に比例して減衰)」の思想と繋がるので覚えやすい
④音圧の記号pと音響パワーの記号Pが同じアルファベットなのが非常に困る
それぞれpressureのpとPOWERのPが由来は分かるけど……もっとこう……あるだろう?
困ったのは、音圧レベルと音響パワーレベルの計算式で音圧はLogの中身がpの2乗で、音響パワーはPの1乗と違う点
理解が十分でない時点での学習ではホント混乱する
「さっきの問題の解説ではpの2乗してたのにこの問題は1乗なのなんで?」と何度かなった
試験お疲れ様でした。
私が作成した解説について、様々にコメントしていただき、運営の参考となりました。
また、コメント返信が遅くなったこと、返信しきれなかったコメントがあったことは、申し訳ありませんでした。
少しでも試験勉強のお役に立てていたようですので、今後の励みになります。
吉報をお祈りしております。
2年ほど前ですが、会社から受験する様にと赤札が届きました。
公式を覚えるのが億劫で諦めていましたが、ピエうさ様のブログのおかけで無事合格できました。
あなたは私の中の神です。
コメントありがとうございます。
つたない解説もあったと思いますが、合格の一助になれて幸いです。
コメントを見受けるところ、周囲の方も公害防止管理者を受験する方がいらっしゃると存じます。
そのような方々に当ブログを紹介していただけると幸いです。
誤記、修正の他、追加の解説なども対応していますので、お気軽にコメントいただければと思います。
会社にプレス機が導入されて、
公害防止管理者 騒音振動の所持者がいないので
会社の指示で勉強中です。
いかんせん、学校卒業して20年以上経過、
logに関してすっかり忘れて一から勉強中です。
解説を読む際、なぜこうなるかとつまずきが多々あり、
なかなか前に進まない状況で苦戦してます。
今回会社において複数人試験を受験しますが、大卒もいれば、工業系高校卒の方もいれ経歴がまちまちで対数を理解していない人もいました。
なら、試験を受験するための基礎知識を紹介してほしいと感じました。対数に関しての最低限の解説、常用対数表の読み方
が欲しいです。
logA^B=BlogA logAB=logA+logB logA/B=logA-logB
ご意見ありがとうございます。
ご要望に添えるか分かりませんが、以下の記事を作成しました。
対数の計算で基礎的な質問がある場合は、以下の記事のコメントに投稿をお願いします。
これで安心!公害防止管理者試験で役立つ常用対数の基礎
https://pierre-usagi.com/db-kiso/
素早い対応に頭が上がりません。
残りあと3週間ですが頑張って勉強します。
ありがとうございました。
突貫工事で作成したので、ご不明点があれば遠慮なくコメントしてください。
おそらく受験生は同じような疑問を持っていることが多いので、皆様の知識向上にも役立つと思います。
引き続き、よろしくお願いします。
弾性支持をしているときの振動伝達率
振動伝達率τ=1/{(f/f₀})²-1}
振動伝達率τ=1/{(f/f₀)²-1}
上記()が重複して「)」側が3個ある
ご指摘ありがとうございます。
記事を修正しましたので、ご確認お願いします。